1.3c Solving Measure of Angles and Number of Sides of Polygons
LEARNING OBJECTIVES
- Determine the measure of angles and number of sides of polygons
Review
Let’s start with a quick refresher on the names of polygons based on their sides. Check out the interactive tool below to jog your memory on polygon names. Have fun exploring!
Do you still remember the Angle Sum Theorem? It tells us that the sum of all interior angles of a polygon can be calculated with this formula, 180°(n-2), where n is the number of sides. This formula works because a polygon can be divided into n−2 triangles, and we know that each triangle has interior angles adding up to 180°. Explore the visual proof below to see this concept in action!
Sample Problems
Example 1
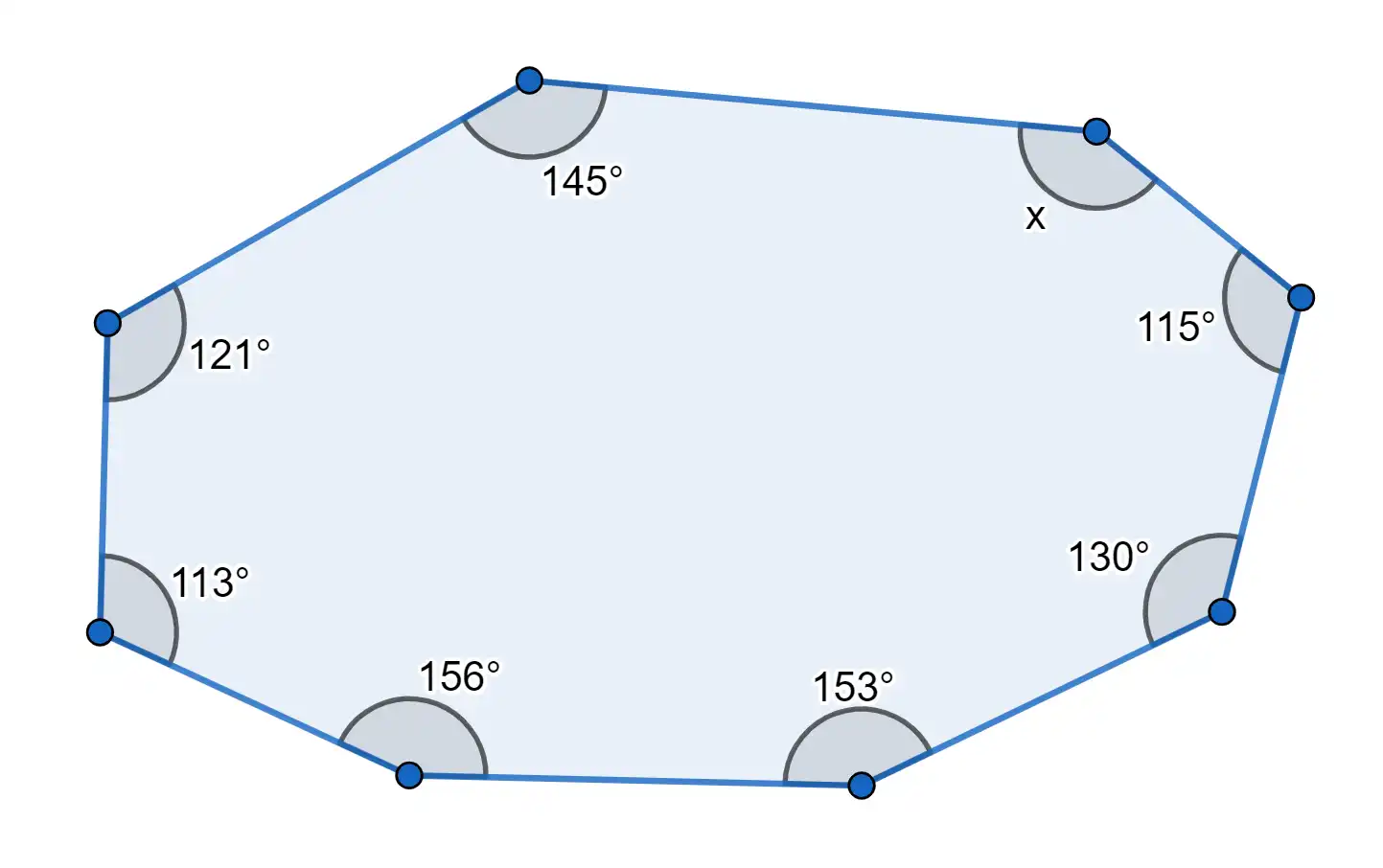
Given the figure at the right, find $ x^\circ $. (Click the image to enlarge.)
- How many sides does the given figure have?
Show Answer
This figure has 8 sides.
- What is the name of the polygon?
Show Answer
This polygons is an octagon.
- What is the sum of its interior angles?
Show Answer
Since it has 8 sides, the sum of its interior angles equals \( (8 - 2)(180^\circ) = 1080^\circ \).
- What is the value of $ x $?
Show Answer
To solve for the value of \( x \), remember that the sum of all the interior angles of an octagon is \( 1080^\circ \). So we add all the interior angles and equate it to \( 1080^\circ \).
Set up the equation: \[ x + 145^\circ + 121^\circ + 113^\circ + 156^\circ + 153^\circ + 130^\circ + 115^\circ = 1080^\circ \]
Combine like terms: \[ x + 933^\circ = 1080^\circ \]
Subtract $ 933 ^\circ $ from both sides: \[ x + 933^\circ - 933^\circ = 1080^\circ - 933^\circ \]
\[ x = 147^\circ \]
Therefore, the missing angle \( x \) is \( 147^\circ \). This makes the total of all the interior angles in the octagon equal to \( 1080^\circ \), just like it should be!
Example 2
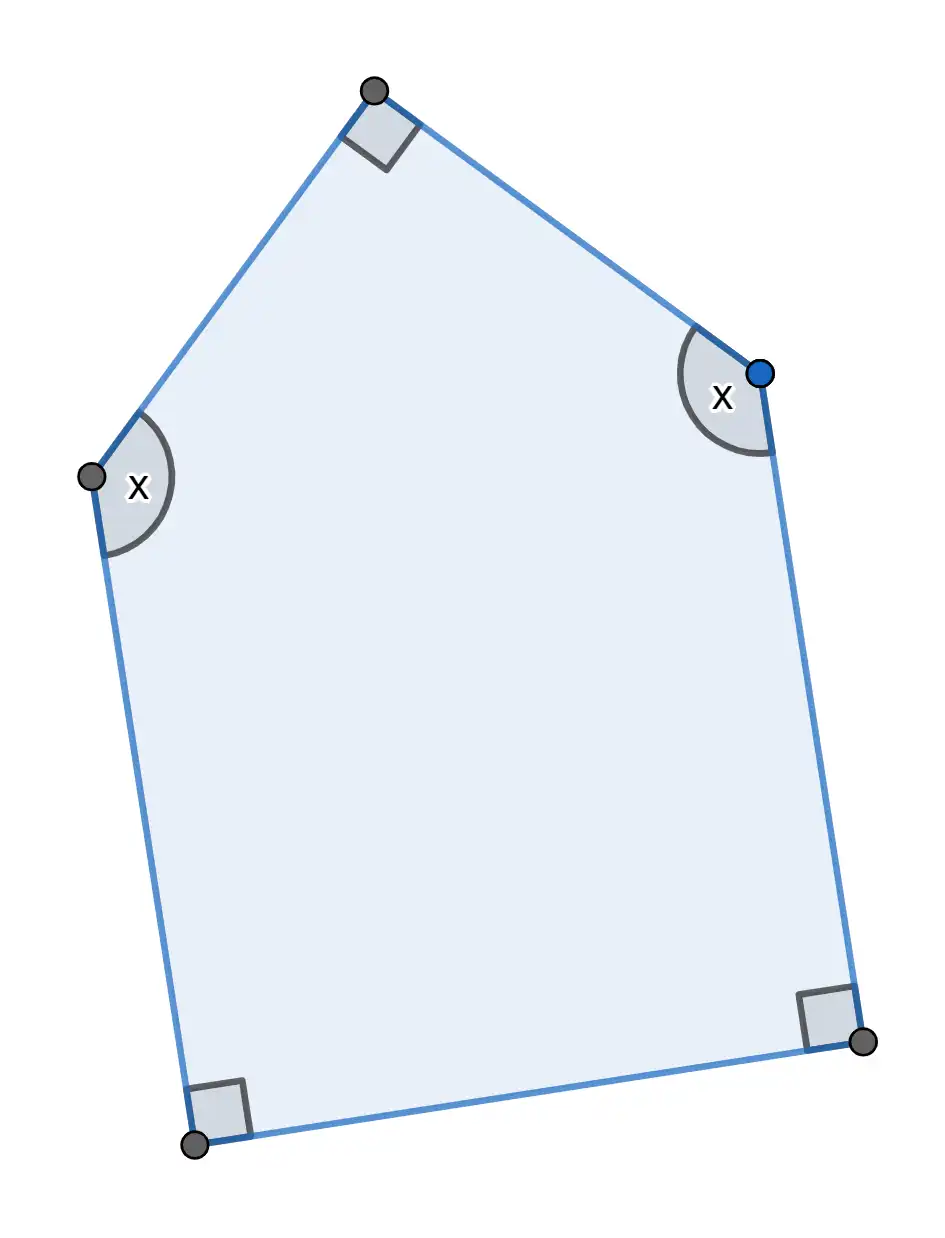
Given the figure at the right, find $ x^\circ $. (Click the image to enlarge.)
- How many sides does the given figure have?
Show Answer
This figure has 5 sides.
- What is the name of the polygon?
Show Answer
This polygons is an pentagon.
- What is the sum of its interior angles?
Show Answer
Since it has 5 sides, the sum of its interior angles equals \( (5 - 2)(180^\circ) = 540^\circ \).
- What is the value of $ x $?
Show Answer
Notice that the other three angles are right angles, meaning each of these angles measures \( 90^\circ \). To find the missing angles, we add all the interior angles and set their total equal to \( 540^\circ \), which is the sum of the interior angles of a pentagon.
Set up the equation: \[ x + x + 90^\circ + 90^\circ + 90^\circ = 540^\circ \]
Combine like terms: \[ 2x + 270^\circ = 540^\circ \]
Subtract \( 270^\circ \) from both sides: \[ 2x + 270^\circ - 270^\circ = 540^\circ - 270^\circ \]
\[ 2x = 270^\circ \]
Divide both sides by 2: \[ x = \frac{270^\circ}{2} = 135^\circ \]
Therefore, the value of \( x \) is \( 135^\circ \). This completes the total interior angles of the pentagon, which equals \( 540^\circ \).
Example 3
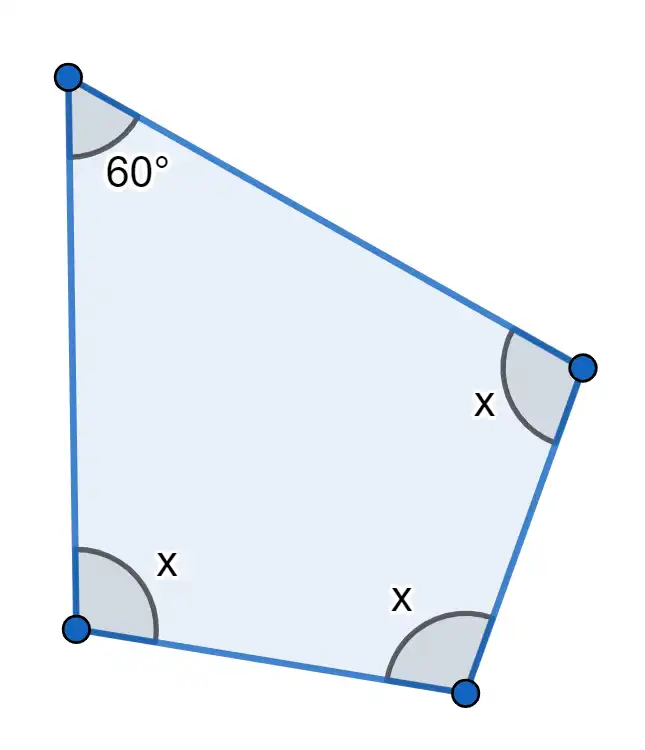
Given the figure at the right, find $ x^\circ $. (Click the image to enlarge.)
- How many sides does the given figure have?
Show Answer
This figure has 4 sides.
- What is the name of the polygon?
Show Answer
This polygons is an quadrilateral.
- What is the sum of its interior angles?
Show Answer
Since it has 4 sides, the sum of its interior angles equals \( (4 - 2)(180^\circ) = 360^\circ \).
- What is the value of $ x $?
Show Answer
To find the missing angles, we add all the interior angles and set their total equal to \( 360^\circ \), which is the sum of the interior angles of a quadrilateral.
Set up the equation: \[ x + x + x + 60^\circ = 360^\circ \]
Combine like terms: \[ 3x + 60^\circ = 360^\circ \]
Subtract \( 60^\circ \) from both sides: \[ 3x + 60^\circ - 60^\circ = 360^\circ - 60^\circ \]
\[ 3x = 300^\circ \]
Divide both sides by 3: \[ x = \frac{300^\circ}{3} = 100^\circ \]
Therefore, the value of \( x \) is \( 100^\circ \). This completes the total interior angles of the quadrilateral, which equals \( 360^\circ \).
Example 4
The sum of all the interior angles of a polygon is $ 1440^\circ $.
- How many sides does the polygon have?
Show Answer
Use the formula for the sum of the interior angles of a polygon:
\[ \text{Sum of interior angles} = (n - 2) \times 180^\circ \]Substitute \( 1440^\circ \) for the sum:
\[ 1440^\circ = (n - 2) \times 180^\circ \]Divide both sides by \( 180^\circ \):
\[ \frac{1440^\circ}{180^\circ} = n - 2 \] \[ 8 = n - 2 \]Add 2 to both sides:
\[ n = 8 + 2 = 10 \]Therefore, the polygon has 10 sides.
- What is the name of the polygon?
Show Answer
Since it has 10 sides, therefore it is a decagon.
Example 5
The measure of one interior angle of a regular polygon is $ 140 ^\circ $. How many sides does the polygon have?
- How many sides does the polygon have?
Show Answer
Use the formula for the sum of the interior angles of a polygon:
\[ \text{Sum of interior angles} = (n - 2) \times 180^\circ \]Since the polygon is regular, the sum of the interior angles can also be expressed as:
\[ \text{Sum of interior angles} = n \times 140^\circ \]Set the two expressions for the sum of the interior angles equal to each other:
\[ (n - 2) \times 180^\circ = n \times 140^\circ \]Expand both sides:
\[ 180n - 360 = 140n \]Simplify by subtracting \( 140n \) from both sides:
\[ 40n - 360 = 0 \]Add \( 360 \) to both sides:
\[ 40n = 360 \]Divide both sides by \( 40 \):
\[ n = \frac{360}{40} = 9 \]Therefore, the polygon has 9 sides.
- What is the name of the polygon?
Show Answer
Since it has 9 sides, therefore it is a nonagon.
- What is the measure of one of its exterior angle?
Show Answer
Recall that the sum of the exterior angles of any polygon is always \( 360^\circ \), and all exterior angles in a regular polygon are equal. To find the measure of one exterior angle, divide \( 360^\circ \) by the number of sides:
\[ \text{One exterior angle} = \frac{360^\circ}{n} \]Step 3: Substitute \( n = 9 \):
\[ \text{One exterior angle} = \frac{360^\circ}{9} = 40^\circ \]Therefore, the measure of one exterior angle is \( 40^\circ \).
Summary
In this lesson, you learned how to calculate the number of sides, the measures of interior angles as well as exterior angles of a polygon. Understanding these concepts helps us see the mathematical patterns in geometric shapes and prepares us for more advanced topics in geometry. Remember, the sum of the interior angles depends on the number of sides and is given by $ (n - 2) \times 180^\circ $ where $ n $ is the number of sides. Additionally, the sum of the exterior angles of any polygon is always $ 360^\circ $. With practice, you’ll master these formulas and be able to solve problems involving polygons with confidence!
Disclaimer: All GeoGebra resources are the intellectual property of their respective creators. Some parts have been modified or adapted for another purpose.