1.2a Convex or Non-Convex Polygon
LEARNING OBJECTIVES
- Describe convex and non-convex polygons.
- Classify polygons whether they are convex or non-convex.
Review
Before we proceed to the main lesson, let us have a recall on the names of polygons. Here are common road signs and markings. Your task is to identify the type of polygon used in each road sign.
Convex and Non-Convex Polygons
Last time we classified polygons whether regular of irregular, we also named them according to the number of sides, now you’ll learn another way of classifying polygon – convex or non-convex. So let us define what is convex and non-convex polygon.
- Convex Polygons
- A convex polygon is a polygon where all interior angles are less than 180 degrees.
- No vertices point inward
- A line segment drawn between any two points in the polygon will always lie inside or on the boundary of the polygon.
- All diagonals are inside the polygon.
- Non-Convex Polygons
- A non-convex or concave polygon is a polygon that has at least one interior angle greater than 180 degrees.
- Has at least one vertex that points inward.
- A line segment drawn between some points within the polygon may pass outside it.
- They are also called as concave polygons.
Examples
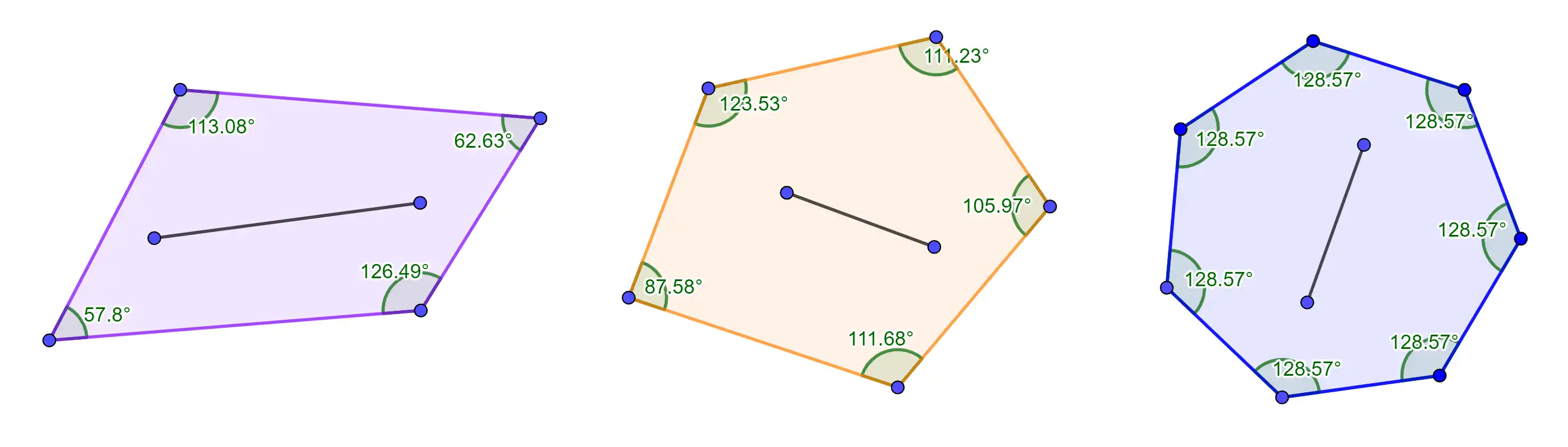 These are examples of convex polygons. If you draw any two points inside the polygon and then connect them, the line segment joining the points is still inside the polygon. Also if you look at the interior angles, all of them are less than 180 degrees.
These are examples of convex polygons. If you draw any two points inside the polygon and then connect them, the line segment joining the points is still inside the polygon. Also if you look at the interior angles, all of them are less than 180 degrees.
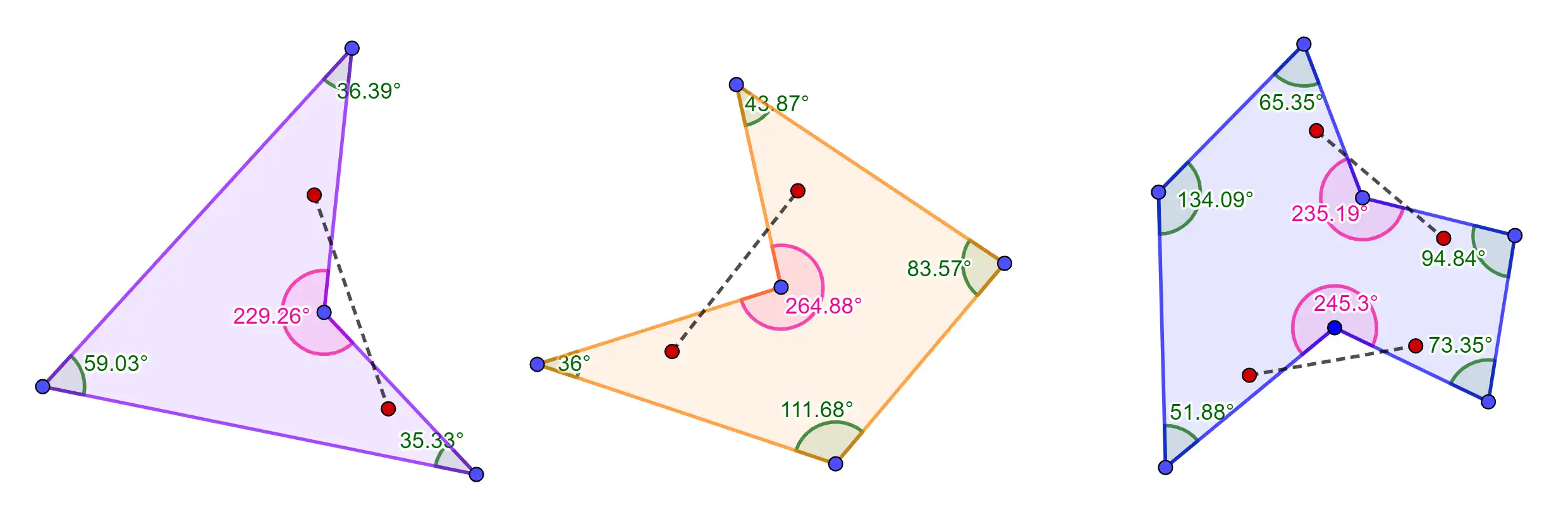 On the other hand, these are examples of non-convex or concave polygons. Notice that there will be instances that when you draw two points and then connect them, some part of the line segment is outside the polygon. This is because the interior angle is greater than 180 degress.
On the other hand, these are examples of non-convex or concave polygons. Notice that there will be instances that when you draw two points and then connect them, some part of the line segment is outside the polygon. This is because the interior angle is greater than 180 degress.
You may explore this Geogebra to better understand what is convex or non-convex polygon. Drag the red points to different directions and notice what happens to the polygon.
Summary
Convex polygons have all their interior angles less than 180 degrees, and no vertices point inward. On the other hand, non-convex (or concave) polygons have at least one interior angle greater than 180 degrees and may have vertices that point inward.
Check Your Understanding
Now that you’ve learned how to classify polygons as convex or non-convex, let’s see if you can apply what you know. Take a look around you—can you find examples of convex or concave polygons in everyday objects? Try drawing them and classify each one.
Disclaimer: All GeoGebra resources are the intellectual property of their respective creators. Some parts have been modified or adapted for another purpose.
