1.1b Interior Angles of Polygons
LEARNING OBJECTIVES
- Identify measure of angles of polygons.
- Determine the measure of each angle of regular polygons.
Review
Let’s see if you still remember the definition and types of polygons as well as naming them according to number of sides. Read the clues and complete the crossword puzzle. You can go back to the previous material if you forgot about them.
Interior Angles of Polygons
As we discussed earlier, the interior angles of a polygon are the angles formed between two adjacent sides inside the polygon. One cool thing about polygons is that the total of these interior angles changes depending on how many sides the polygon has. But before we get into that, let us review how to measure an angle using a protractor by watching this video.
Interior Angles of a Triangle
Now that you understand how to measure angles, let’s explore the interior angles of a polygon, starting with the simplest polygon: the triangle. If you measure each of the three interior angles and add them up, you’ll find that their sum is always \(180^\circ\), regardless of the type of triangle.
Interior Angles of Quadrilaterals
Next, consider a quadrilateral, which is any polygon with four sides. A common example is a square. A square is a regular quadrilateral, meaning all its sides and angles are equal. Since each angle in a square is a right angle, measuring \(90^\circ\), the total sum of the interior angles in a square is:
\[90^\circ \times 4 = 360^\circ\]This sum, \(360^\circ\), is consistent for all quadrilaterals, not just squares.
Interior Angle Sum Formula
To find the sum of the interior angles of any polygon, you can use the following formula:
\[\text{Sum of interior angles} = (n-2) \times 180^\circ\]Where \(n\) is the number of sides of the polygon. This formula works because any polygon can be divided into triangles, and each triangle contributes \(180^\circ\) to the total sum. For instance in quadrilaterals, we can divide any quadrilateral into two triangles. Therefore, \(180^\circ\times 2 = 360^\circ\) is the sum of all interior angles of quadrilaterals.
Interior Angles of Pentagons
For a pentagon, which has 5 sides:
\[\text{Sum of interior angles} = (5-2) \times 180^\circ = 3 \times 180^\circ = 540^\circ\]This means that the sum of all interior angles in a pentagon is \(540^\circ\). Again, this formula works because we can divide any pentagon into three triangles like the figure below.
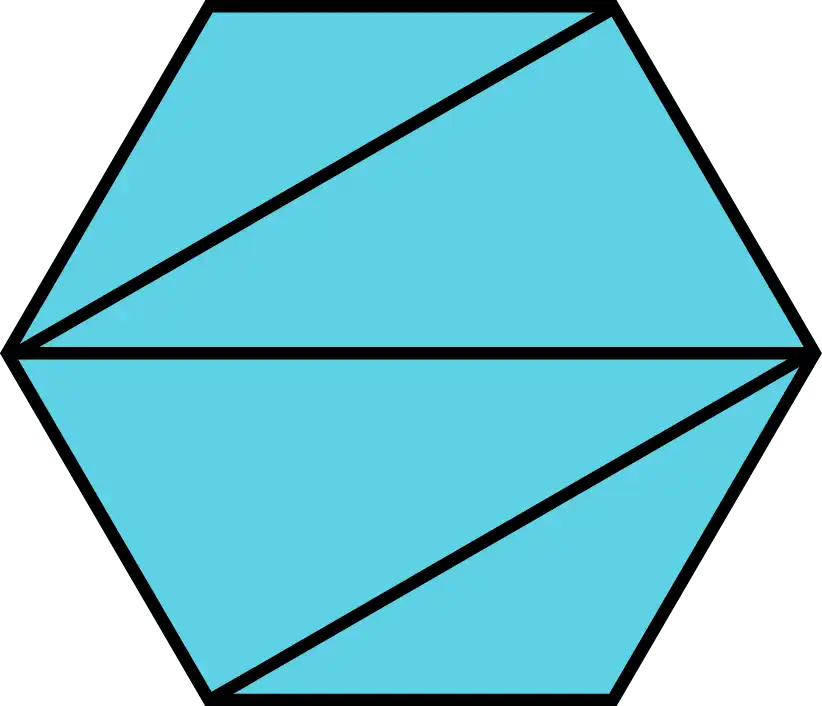
Interior Angles of Hexagons
For a hexagon, which has 6 sides:
\[\text{Sum of interior angles} = (6-2) \times 180^\circ = 4 \times 180^\circ = 720^\circ\]Thus, the interior angles of a hexagon add up to \(720^\circ\). Following the same logic for the quadrilateral and pentagon, we can divide any hexagon into four triangles.
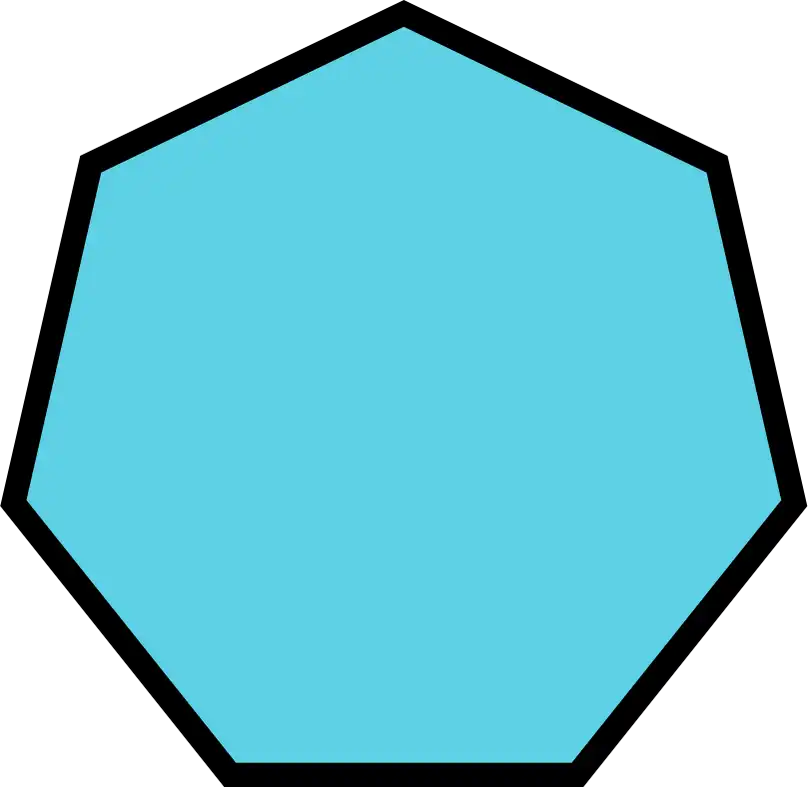
Interior Angles of Heptagons
For a heptagon, which has 7 sides:
\[\text{Sum of interior angles} = (7-2) \times 180^\circ = 5 \times 180^\circ = 900^\circ\]The sum of all interior angles in a heptagon is \(900^\circ\). Can you also try to divide this heptagon into triangles? How many triangles did you make?
Interior Angles of Octagons
For an octagon, which has 8 sides:
\[\text{Sum of interior angles} = (8-2) \times 180^\circ = 6 \times 180^\circ = 1080^\circ\]The interior angles of an octagon sum to \(1080^\circ\). Again, try to divide this octagon into triangles. How many triangles did you make?
Interior Angles of Nonagons
For a nonagon, which has 9 sides:
\[\text{Sum of interior angles} = (9-2) \times 180^\circ = 7 \times 180^\circ = 1260^\circ\]Therefore, the interior angles of a nonagon add up to \(1260^\circ\). Let us verify again this formula by dividing this nonagon into triangles. How many triangles did you make?
Interior Angles of Decagons
Finally, for a decagon, which has 10 sides:
\[\text{Sum of interior angles} = (10-2) \times 180^\circ = 8 \times 180^\circ = 1440^\circ\]So, the sum of all interior angles in a decagon is \(1440^\circ\). Again, to verify this formula, consider this decagon. Into how many triangles can you divide this decagon?
Determining Each Interior Angle of a Regular Polygon
Knowing the total measure of the interior angles of a polygon, we can use this to determine the measure of each angle in a regular polygon. Remember that regular polygons are polygons with equal sides and equal angles. So, if we know the sum of the interior angles, we can simply divide this sum by the number of angles (which is the same as the number of sides) to find the measure of each interior angle. For example, in a regular hexagon (which has 6 sides), the sum of the interior angles is \(720^\circ\). Dividing this by 6 gives us:
\[\frac{720^\circ}{6} = 120^\circ\]So, each interior angle in a regular hexagon measures \(120^\circ\). See the summary table below.
Summary Table
| Polygon | Number of Sides (n) | Each Interior Angle of a Regular Polygon | Sum of Interior Angles |
|---|---|---|---|
| Triangle | 3 | 60° | 180° |
| Quadrilateral | 4 | 90° | 360° |
| Pentagon | 5 | 108° | 540° |
| Hexagon | 6 | 120° | 720° |
| Heptagon | 7 | \(\approx\)128.57° | 900° |
| Octagon | 8 | 135° | 1080° |
| Nonagon | 9 | 140° | 1260° |
| Decagon | 10 | 144° | 1440° |
| Any polygon | \(n\) | \(\frac{(n-2) \times 180}{n}^\circ\) | \((n-2) \times 180^\circ\) |