1.1a Properties and Classifications of Polygons
LEARNING OBJECTIVES
- Define a polygon and describe its properties.
- Classify polygon according to number of sides.
- Name polygon and its parts.
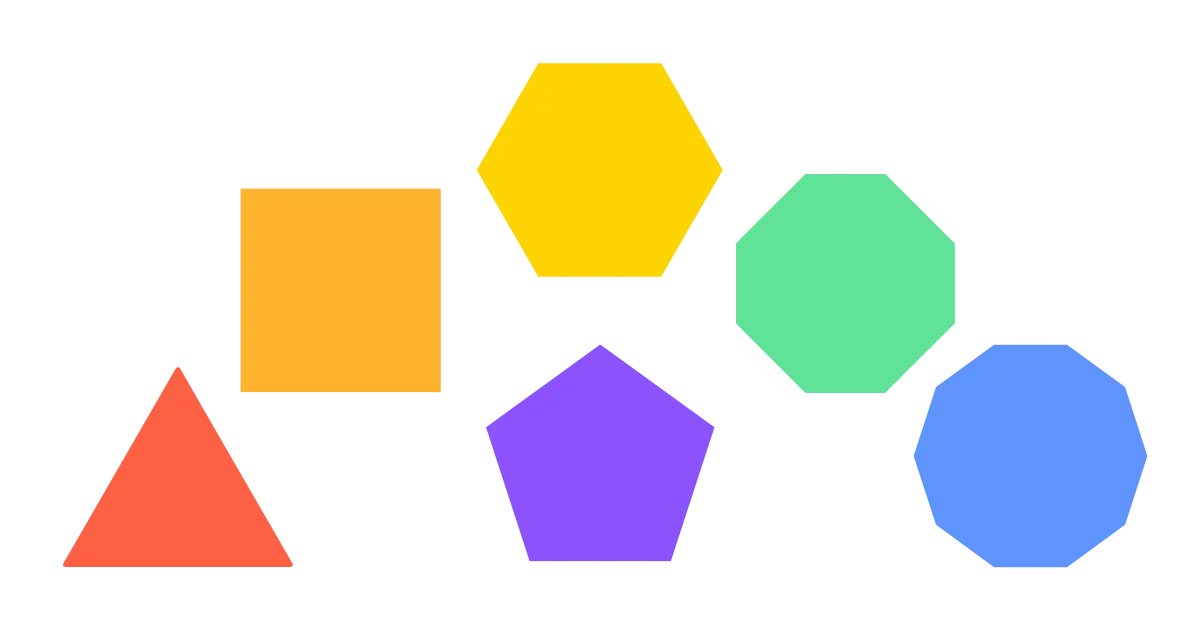
What is a Polygon?
A polygon is a flat shape with straight sides. The sides must intersect only at the endpoints to form a closed figure. Here are some common polygons:
Activity: Classification of Polygons According to Number of Sides
Take a moment to review how polygons are classified based on their number of sides. Do the activity below
🔎 Show explanation of the answers
How did you find the activity? I hope you achieved a perfect score!
Notice that the name of the polygon starts with a Greek or Latin prefix that corresponds to the number of sides. Here are some common prefixes:
- Tri - for 3 sides = Triangle
- Quadri (or Tetra) - for 4 sides = Quadrilateral
- Penta - for 5 sides = Pentagon
- Hexa - for 6 sides = Hexagon
- Hepta - for 7 sides = Heptagon
- Octa - for 8 sides = Octagon
- Nona - for 9 sides = Nonagon
- Deca - for 10 sides = Decagon
By now, you should know how polygons are classified based on their number of sides. Let us move forward and explore the different types of polygons.
Types of Polygons
| Type of Polygon | Definition |
|---|---|
 | Equilateral Polygon is a polygon whose sides are all congruent. |
 | Equiangular Polygon is a polygon whose angles are all congruent. |
 | Regular Polygon is a polygon that is both equilateral and equiangular. |
 | Irregular Polygon is a polygon whose sides and angles are not equal. |
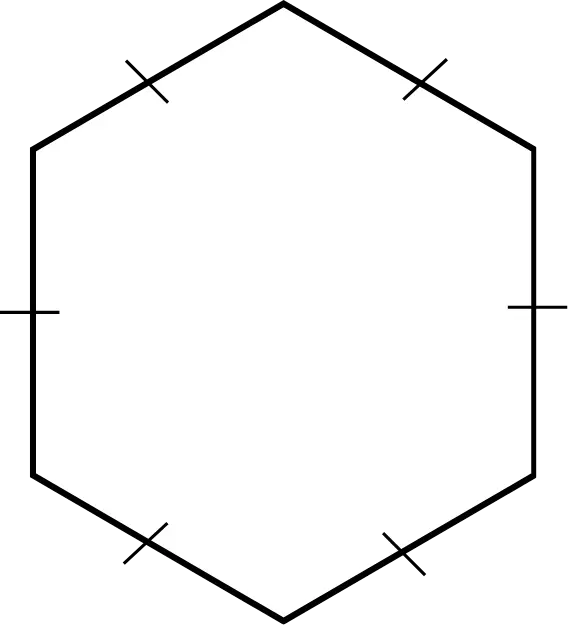
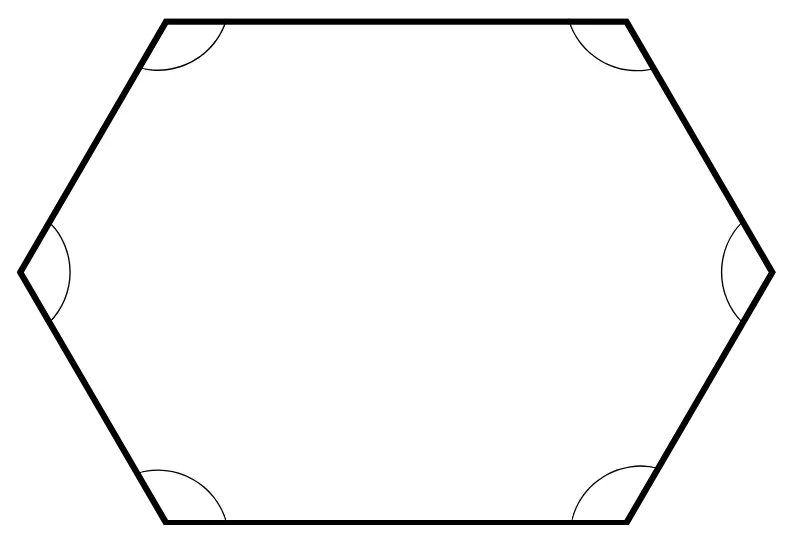
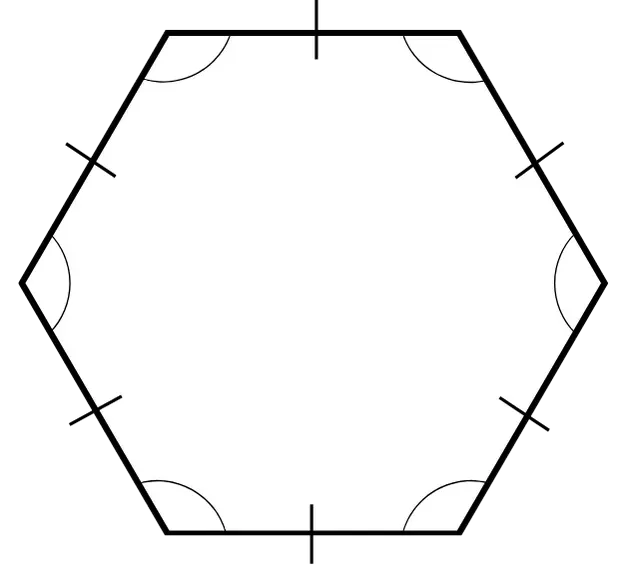
The tick marks on sides indicate congruence, meaning the sides are of equal length. Similarly, small arcs indicate that the angles are congruent. The number of tick marks and small arcs may vary to represent different pairs of congruent sides or angles.
Activity: Polygon or NOT
Let us have a short activity. Which among the following figures are polygons? Click the correct figures.
🔎 Show explanation of the answers
Remember our definition of polygons. Polygons are closed, plane figures, made of line segments, and the segments intersect only at their end points. The figures below are polygons.
The figures below are not polygons. The first figure is not a flat figure,the second and third figure have sides that intersect at a point other than the endpoints, the fourth figure is not closed, and the last one has curve.
Can you think of other figures that are not polygons? Draw them on your notebook.
Naming Polygon and its Parts
Let’s start by examining the components of a polygon.
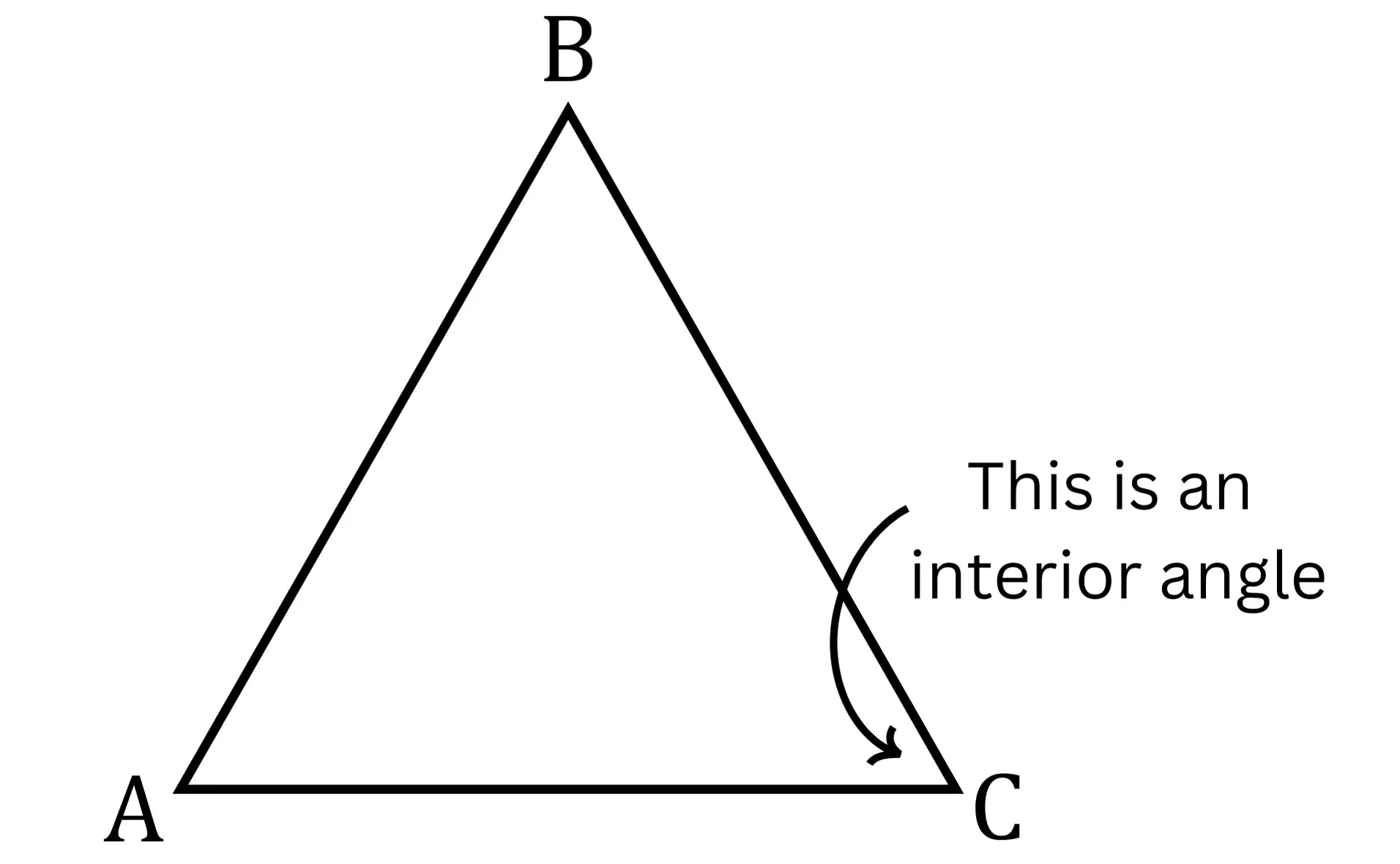
Consider a triangle. A triangle is a basic polygon with three sides and three interior angles. Here’s how we describe and name its parts:
Vertices: These are the points where a polygon’s sides meet. We name these vertices with capital letters. In our example, the vertices are points \(\text{A}\), \(\text{B}\), and \(\text{C}\).
Naming the Triangle: The triangle can be named using its vertices. The order of the vertices can vary, so this triangle can be referred to as: \(\triangle \text{ABC}\), \(\triangle \text{BCA}\), or \(\triangle \text{ACB}\). Each name represents the same triangle but emphasizes a different vertex order.
Sides: The sides of a triangle are the line segments connecting the vertices. For triangle \(\triangle \text{ABC}\), the sides are: \(\overline{\text{AB}}\), \(\overline{\text{BC}}\), and \(\overline{\text{AC}}\). Each line segment connects two of the vertices and forms part of the triangle’s perimeter.
Interior Angles: The interior are the angles formed inside a polygon where two adjacent sides meet. For triangle \(\triangle \text{ABC}\), the interior angles are: \(\angle \text{BAC}\), \(\angle \text{BCA}\), and, \(\angle \text{ABC}\). Each angle is named based on its vertex and the sides forming it.
Activity: Naming Polygon and its Parts
In this lesson, we defined a polygon. We covered the key properties of polygons, including their sides, vertices, and interior angles. We also discussed how to name polygons and its parts.
To identify if it is a polygon, just verify using this checklist:
- closed
- flat
- straight sides
- intersect only at the endpoints